9 July 2022

Математичні формули в Markdown для Github pages

by Pavlo Shcherbukha

Вступ

На написання цього блогу спонукало широке використання markdown в технічній документації в багатьох технічних дисциплінах, що пов’язані з IT. Знову ж таки, github pages стали у більшості випадків основним ресурсом для обміну знаннями. Ососбисто я, в більшості випадків, відмовися від продуктів MS Office на користь Markdown і пишу технічні специфікації з використанням markdown. Ну і команда в своїй роботі використовує git lab, що встановлено локально, тому github pages та gitlab pages стали основним інструментом для поширення знань в команді. А вміння писати формули в markdown важливо, тому, що можеш комфортно описувати свої думки у звичному форматі.

Основним відбправним елементом для розуміння як це зробити було посилання:

How to use MathJax in Jekyll generated Github pages

pic-01

Я спробував зробити так, як написано,

pic-02

але з першого ж кроку отримав помилку при building gitpages:

Error: You're using the 'maruku' Markdown processor, which has been removed as of 3.0.0. We recommend you switch to Kramdown. To do this, replace markdown: maruku with markdown: kramdown in your _config.yml file.
Logging at level: debug
Configuration file: /github/workspace/./_config.yml

Заміна на Kramdown не принесла якогось виграшу, але, якщо у вас багато написано, то заміна markdown-процесора може привести до не очікуваних результатів. Але, кому цікаво, то можна прочитати про markdown процессори за лінками:

Кramdown постачається під ліцензією MIT та може бути використаний в комерційних проектах.

Maruku

Якщо почитати порівняльну статтю compare-maruku-vs-kramdown, то , на мій погляд, kramdown швидко розвивається, а maruku - занепадає.

Висновок:

markdown процесор - цікаво, але для вирішення задачі вводу матетматичних формул воно великого значення не має.

Наступною порадою в цій статті було використання mathjax: mathjax. Це JavaScript двигун, для відображення в браузерах математичних формул, що написані в форматі markdown. Ну, а документація, як його підключити, описана за лінком: http://docs.mathjax.org/en/latest/web/configuration.html. Якщо порівняти зі статтею, на яку я посилався, то можна зрозуміти, що опис підключення відрізняється. Стаття написана під стару версію mathjax, яка вже не працює.

Висновок:

mathjax - це основна річ, але її потрібно підключити до мого github pages.

В статті пропонується модифікувати основний шаблон github pages, та додати стилі і блок умовного використання mathjax

pic-04

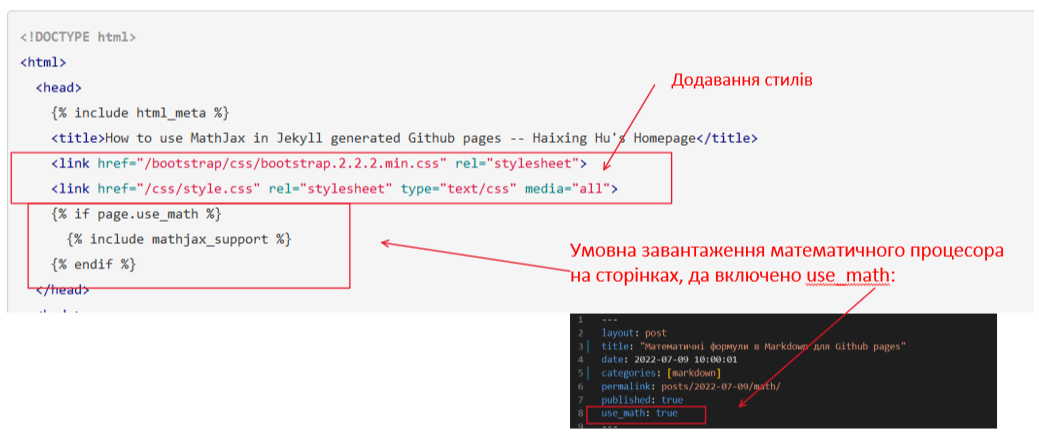
Стилі, як виявилися, не мають ключового значення для відображеня формул, а от завантаження потрібної сторінки - це важливо.

Також, цікавим було посилання, з приводу правил написання математичних формул:

https://github.blog/2022-05-19-math-support-in-markdown/
https://docs.github.com/en/get-started/writing-on-github/working-with-advanced-formatting/writing-mathematical-expressions

Основним рухаючим фактором для підключеня можливості відображення математичних формул в блогах є mathjax для сайтів, що згенеровані за допомогою Jekyll.

Підключення mathjax до Jekyll генератора для github pages

Створення завантажувача mathjax

Перше, що потрібно зробити, це створити сторінку-завантажувач mathjax в катлозі _includes. Для цього створено файл mathjax_support.html з таким текстом:

<script>
  MathJax = {
    tex: {
      inlineMath: [['$', '$'], ['\\(', '\\)']]
    },
    svg: {
      fontCache: 'global'+
    }
  };
  </script>


<script type="text/javascript" id="MathJax-script" async
  src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-svg.js">
</script>

По суті, текст повторює рекомнедацію з документації за лінком: http://docs.mathjax.org/en/latest/web/configuration.html.

Доопрацювати шаблон github pages для заватнаження mathjax_support.html.

Зазвичай шаблон github pages знаходиться в каталозі _layouts і називається default.html. В розділ head потрібно додати умовне завантаження бібліотеки:

   
      
<script>
  MathJax = {
    tex: {
      inlineMath: [['$', '$'], ['\\(', '\\)']]
    },
    svg: {
      fontCache: 'global'
    }
  };
  </script>


<script type="text/javascript" id="MathJax-script" async
  src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-svg.js">
</script>
   

pic-05

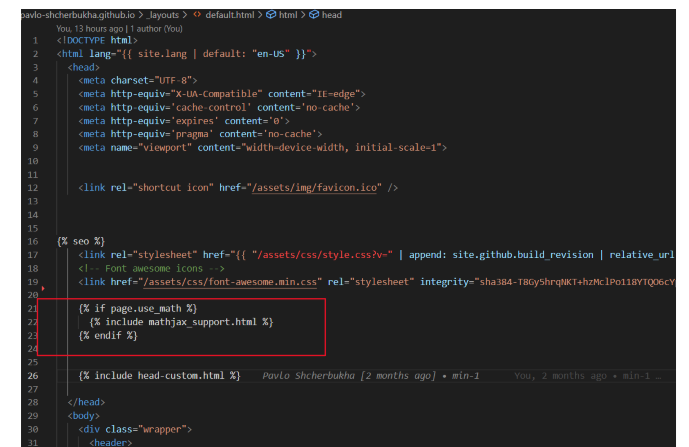
Підготувати блог і в ньому включити завантаження MathJax

Коли створюємо блог, то до заголовку блога потрібно додати: use_math: true, як показано нижче:

---
layout: post
title: "Математичні формули в Markdown для Github pages"
date: 2022-07-09 10:00:01
categories: [markdown]
permalink: posts/2022-07-09/math/
published: true
use_math: true
---

В принципі все. цього достатньо.

Пробуємо відображення формул в блозі

проста формула в inline, що починається з роздільника “$” виглядає таким чином:

$\sqrt{3x-1}+(1+x)^2$

відображається в рядку тесту $\sqrt{3x-1}+(1+x)^2$ от так.

Формули, що відображаються в окремому блоці з використанням блока “формула”:
опис формули

$$\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)$$

відображення формули в окремому математичному блоці

\[\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)\]

опис формули

      $$\sqrt{3x-1}+(1+x)^2$$

відображення в математичному блоці

\[\sqrt{3x-1}+(1+x)^2\]

опис формули


$$Y=X/(5+ Y^2)$$

відображення в математичному блоці

\[Y=X/(5+ Y^2)\]

опис формули

$$
   |\psi_1\rangle = a|0\rangle + b|1\rangle
$$

відображення в математичному блоці

\[|\psi_1\rangle = a|0\rangle + b|1\rangle\] tags: